Normalization models - introduction
The following chapters discuss some general aspects of the normalization and the different normalization models in nevisDetect. We assume some familiarity of the user with machine learning / statistics.
Notation
- The plug-in risk score of the plug-in i will be denoted by a subscript: ri
- The vector of all plug-in risk scores will be denoted by r: r = (r1, ...rD) where D denotes the number of plug-in risk scores.
- The normalized risk score will be denoted by rnormalized . The normalization itself will be denoted by the function N: rnormalized = N(r1, ...rD) or rnormalized = N(r) in vector notation.
- In a set of plug-in risk scores, the single plug-in risk scores will be denoted by an upper index: { r (1) , r (2) ... , r (n) }
Desired properties of the normalization
From a security point of view the normalization should have the following properties:
- If at least one of the plug-in risk scores increases, the normalized risk score should also increase. (Monotonicity property)
- The proximity of several plug-in risk scores should reduce the value of the normalized risk score. (Proximityproperty)
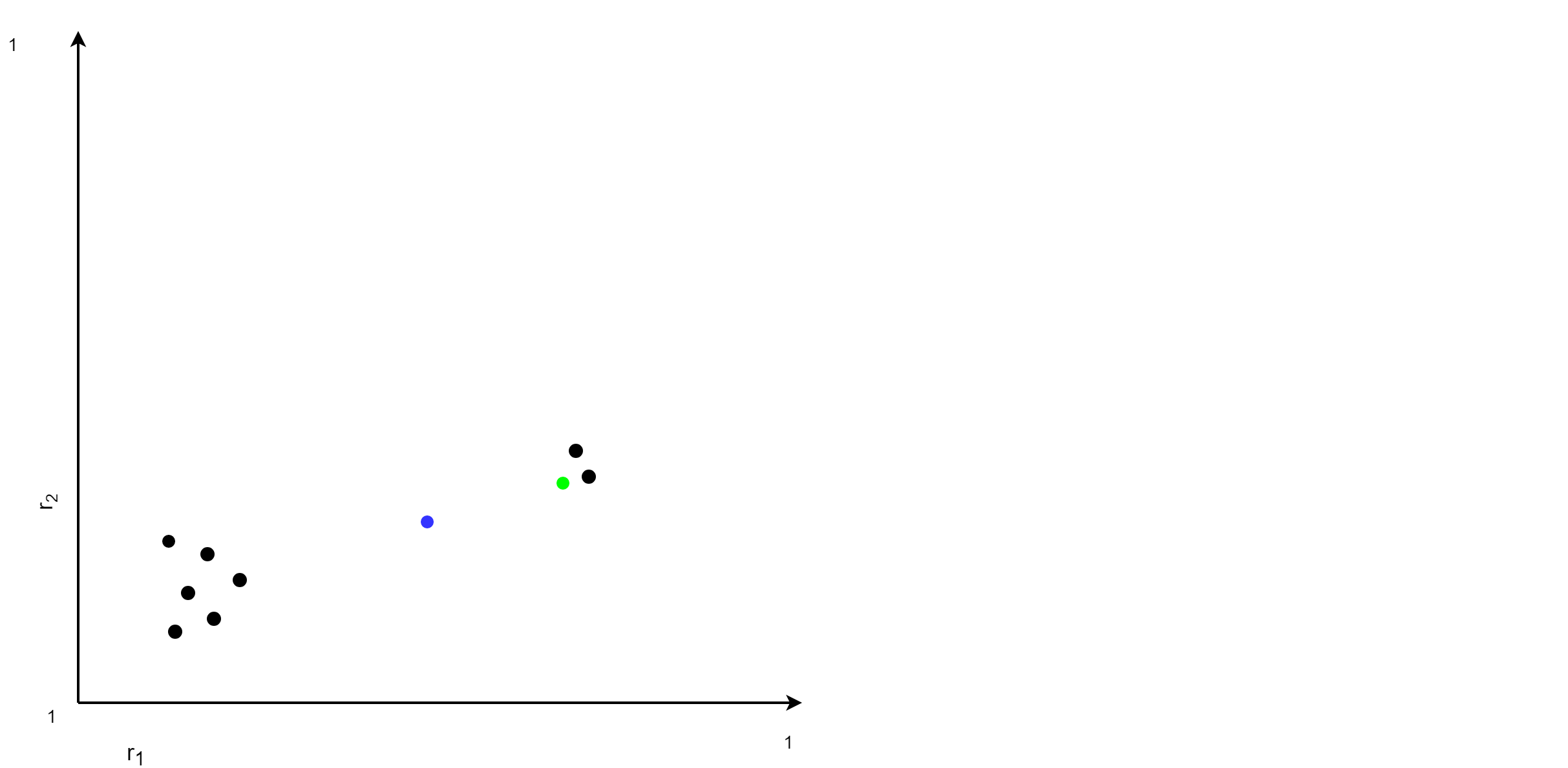
The two requirements are in general contradictory, as the following picture points out: The black points are the plug-in risk scores that have been observed in the past. Now lets compare the normalized risk score of the blue and the green point. According to the Monotonicity property, the normalized risk score of the green point should be larger then the one of the blue point since all it's plug-in risk scores are larger. On the other hand, the Proximity property requires the opposite since the green point is quite close to other points.
See the normalization model described in the chapter Probability density based model for details.
Machine learning formulation
In terms of Machine Learning, we state the normalization as follows:
- The plug-in risk scores are the observed variables. Since we do not have any labels on the data we have an unsupervised problem.
- We assume a latent or hidden random scalar variable z. The data generating process is given by a mapping f from the latent space to the observed variable space: r = f(z) + ε; where ε is a zero-mean multivariate noise variable
- The normalized risk score is determined by the probability of the latent variable z~ corresponding to the observed variable r~. (The reverse mapping f-1 is not unique. Given r~ we choose the z~ with the largest probability.)
The following picture gives an schematic view:
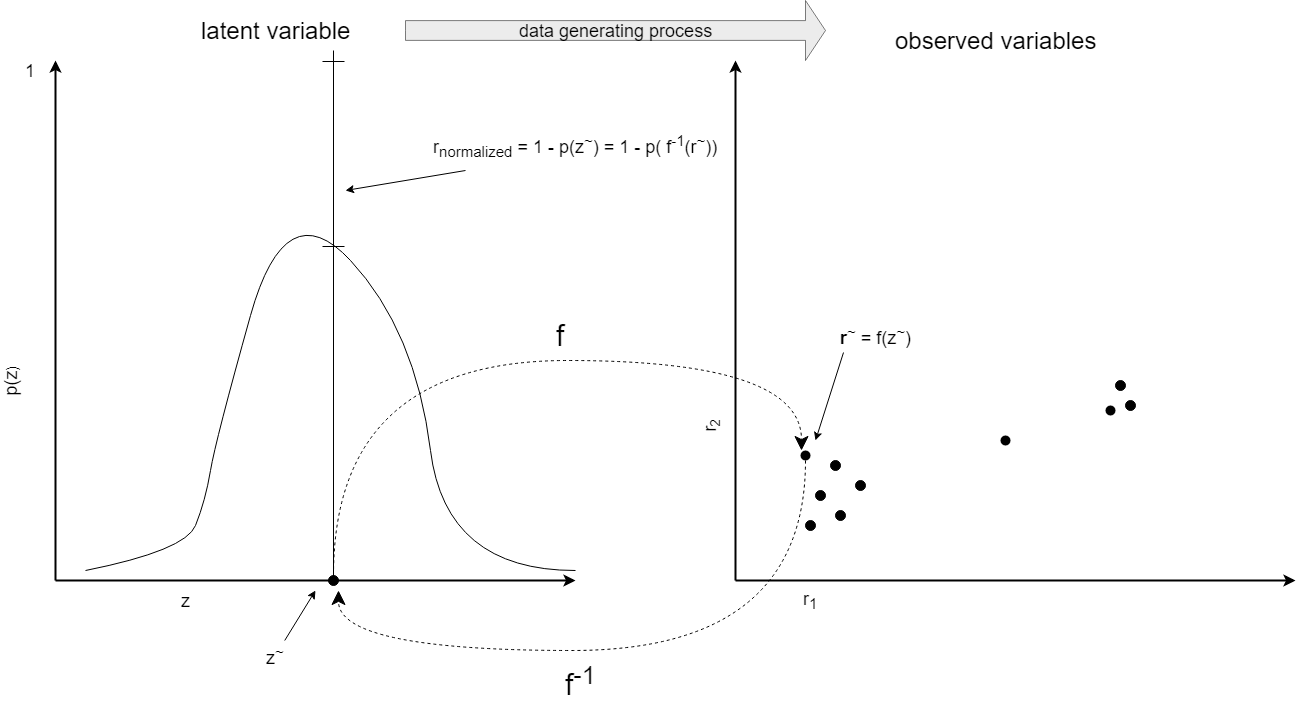
Without loss of generality we can assume that the latent variable z is normal distributed with a zero mean. The task of learning the normalization then consists of:
- Learning the reverse mapping f-1
- Learning the variance of the distribution of the latent variable.
To see where in the Machine Learning landscape the normalization problem resides, we make the following simplifications:
- The mapping f is affine: r = w · z + a + ε with some D-dimensional weight vectors w and a.
- The noise ε is a zero-mean multivariate normal distributed.
In that case, the above formulation of the normalization is a Probabilistic Principal Component Analysis. From a practical point of view, a Probabilistic Principal Component Analysis is not meaningful (the space of the latent variable z is 1-dimensional and so the resulting distribution of p(r) is a multivariate normal distribution centered on the mean of the training data).
Global and user-specific normalization
In general, we can distinguish between a global and user-specific model. To make the difference clear, let's assume for simplicity that we have a parametric model rnormalized = N(r; θ), with some parameter vector θ.In case of the global model, we use a training data set containing data points from all users to learn the parameter vector θ. For the user-specific model, we use a training data set that only contains data points from a specific user. From a machine learning point of view, there is no difference between the global and the user-specific model.
From a security point of view, a user-specific model is preferred: In the end we will define some actions based on the magnitude of the normalized risk score computed for a certain HTTP of a user. In case of a global model, the normalized risk scores of certain users may have some bias because the used plug-in risk scores have some bias.
But beside the security aspect also the computational aspect has to be taken into account: In case of the user-specific model, both the time needed for training the model and the size of the model parameters are critical factors.
In nevisDetect currently only global models are supported.