Probability density based model

In the normalization model described here we make the assumption that the plug-in risk scores are statistically independent: p(r) = p₁(r₁) · p₂(r₂) · ... · p_D(r_D). The normalized risk score is defined as r_normalized = 1 - p₁(r₁) · p₂(r₂) · ... · p_D(r_D) = 1 - p(r).

Since we would like to make full use of the interval from 0.0 to 1.0 for the normalized risk score, we scale p₁(r₁) · p₂(r₂) · ... · p_D(r_D) by it's mode: r_normalized= 1 - p₁(r₁) · p₂(r₂) · ... · p_D(r_D) / (mode₁ · mode₂ · ... · mode_D) , with mode_i as the mode of the density p_i.

We estimate the single densities pi from the observed data by a kernel density estimator using a Gaussian kernel. The bandwidth h_i of the kernel estimating p_i is by default chosen as: h_i = 3 · s²(p_i) , where s² denotes the empirical variance of the observed data. (The factor 3 can be replaced by any other value by configuration.)

The following pictures show 657 data points of BehavioSecSession and BehavioSecTransaction plug-in risk scores (denoted by r₁ and r₂) from a nevisDetect test system and a level plot of the trained normalization:

Note that the data are not realistic, since the test system has frequently being used for demonstration purposes with a confidence threshold of 0.0.

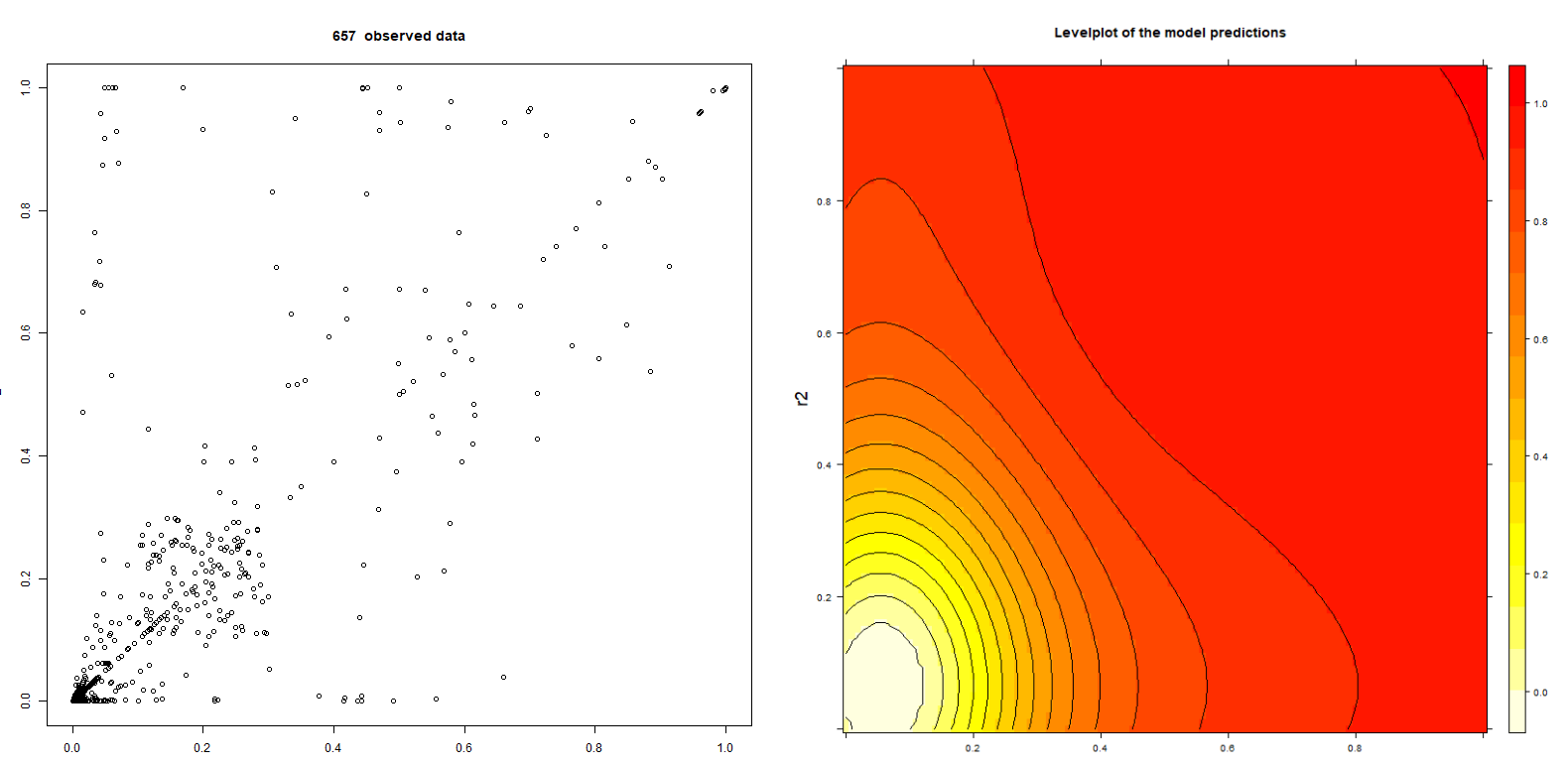
The advantages of the probability density based model are:

• Training the model is fast, stable, and also suited for a large training data set.
• The Proximity property is fulfilled.

The disadvantages are:

• The assumption of statistical independence of the plug-in risk scores does not hold.
• The desired property of Monotonicity is in general not fulfilled.